Uji Homogenitas Dengan SPSS

Uji homogenitas dimaksudkan untuk memperlihatkan bahwa dua atau lebih kelompok data sampel berasal dari populasi yang memiliki variansi yang sama. Pada analisis  regresi, persyaratan analisis yang dibutuhkan adalah bahwa galat regresi untuk setiappengelompokan berdasarkan variabel terikatnya memiliki variansi yang sama. Hipotesis yang diuji adalah sebagai berikut :

H1 : Salah satu tanda = tidak berlaku

Teknik pengujian yang digunakan adalah Uji Bartlet. Uji Bartlet dilakukan dengan menghitung x². Harga x² yang diperoleh dari perhitungan (x²_hitung) selanjutnya dibandingkan dengan x² dari tabel (x²_tabel ), bila x²_hitung < x²_tabel , maka hipotesis nol diterima. Artinya data berasal dari populasi yang homogen.

Uji Homogenitas Pada Uji Perbedaan

Uji homogenitas pada uji perbedaan (seperti anava) dimaksudkan untuk menguji bahwa setiap kelompok yang akan dibandingkan memiliki variansi yang sama. Dengan demikian perbedaan yang terjadi dalam hipotesis benar-benar berasal dari perbedaan antara kelompok, bukan akibat dari perbedaan yang terjadi di dalam kelompok. Misalkan Suatu penelitian ingin membandingkan tingkat kemandirian anak (Y) berdasarkan kelompok daerah, yaitu pedesaan (X1), pinggiran kota (X2), dan perkotaan (X3).

Uji Homogenitas Regresi

Uji homogenitas untuk persyaratan analisis regresi menggunakan teknik yang sama dengan uji homogenitas untuk persyaratan uji perbedaan. Perbedaannya terletak pada cara pengelompokan data variabel terikat. Jika pada uji perbedaan, pengelompokan data variabel terikat didasarkan pada kelompok sampel, maka pada uji homogenitas pada uji regresi, pengelompokan data variabel terikat dilakukan berdasarkan data varaibel bebas.

Uji Homogenitas dengan SPSS

1. Langkah-langkah pengujian homogenitas dengan SPSS
   Untuk menguji kehomogenan data sampel y berdasarkan pengelompokan data X, lakukan langkah-langkah berikut.
   • Buka file data yang akan dianalisis
   • Pilih menu berikut ini
     Analyze–>Descriptives Statistics–>Explore
   • Pilih y sebagai dependent list dan x sebagai faktor list
     Catatan: Untuk homogenitas uji beda, x adalah kode kelompok Untuk homogenitas regresi, x adalah prediktor
   • Klik tombol Plots
   • Pilih Lavene test, untuk untransformed
   • Klik Continue lalu klik OK
     Untuk keperluan penelitian, pada umumnya hanya perlu keluaran Test of Homogenity of Variance. Keluaran lain bisa dihapus dengan cara klik sekali pada objek yang dihapus, lalu tekan tombol Delete.
2. Menafsirkan hasil uji homogenitas
   • Tetapkan taraf signifikansi uji, misalnya α = 0,05
   • Bandingkan p dengan taraf signifikansi yang diperoleh
   • Jika signifikansi yang diperoleh > α, maka variansi setiap sampel sama
     (homogen)
   • Jika signifikansi yang diperoleh < α, maka variansi setiap sampel tidak sama
     (tidak homogen)
     Ternyata pengujian dengan statistik Based on Mean diperoleh signifikansi 0,907,
     jauh lebih melebihi 0,05. dengan demikian data penelitian di atas homogen.
   • Tetapkan taraf signifikansi uji, misalnya α = 0,05
   • Bandingkan p dengan taraf signifikansi yang diperoleh
   • Jika signifikansi yang diperoleh >α, maka variansi setiap sampel sama (homogen)
   • Jika signifikansi yang diperoleh <α, maka variansi setiap sampel tidak sama (tidak homogen)
   Ternyata pengujian dengan statistik Based on Mean diperoleh signifikansi 0,907, jauh lebih melebihi 0,05. dengan demikian data penelitian di atas homogen.
   • Tetapkan taraf signifikansi uji, misalnya α = 0,05
   • Bandingkan p dengan taraf signifikansi yang diperoleh
   • Jika signifikansi yang diperoleh >α, maka variansi setiap sampel sama (homogen)
   • Jika signifikansi yang diperoleh <α, maka variansi setiap sampel tidak sama (tidak homogen)
   Ternyata pengujian dengan statistik Based on Mean diperoleh signifikansi 0,907, jauh lebih melebihi 0,05. dengan demikian data penelitian di atas homogen.
   • Tetapkan taraf signifikansi uji, misalnya α = 0,05
   • Bandingkan p dengan taraf signifikansi yang diperoleh
   • Jika signifikansi yang diperoleh >α, maka variansi setiap sampel sama (homogen)
   • Jika signifikansi yang diperoleh <α, maka variansi setiap sampel tidak sama (tidak homogen)
   Ternyata pengujian dengan statistik Based on Mean diperoleh signifikansi 0,907, jauh lebih melebihi 0,05. dengan demikian data penelitian di atas homogen.
   • Tetapkan taraf signifikansi uji, misalnya α = 0,05
   • Bandingkan p dengan taraf signifikansi yang diperoleh
   • Jika signifikansi yang diperoleh >α, maka variansi setiap sampel sama (homogen)
   • Jika signifikansi yang diperoleh <α, maka variansi setiap sampel tidak sama (tidak homogen)
   Ternyata pengujian dengan statistik Based on Mean diperoleh signifikansi 0,907, jauh lebih melebihi 0,05. dengan demikian data penelitian di atas homogen.
Sebagai contoh, pada kesempatan ini diuji homogenitas data uji perbedaan tingkat kemandirian anak (Y) berdasarkan kelompok daerah, yaitu pedesaan (X1), pinggiran kota (X2), dan perkotaan (X3), yang telah diuji secara manual dengan uji Bartlet sebelumnya. Hasil analisis adalah seperti tercantum pada gambar berikut.



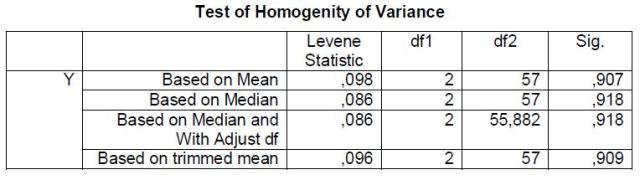
Interpretasi dilakukan dengan memilih salah satu statistik, yaitu statistik yang didasarkan pada rata-rata (Based on Mean). Hipotesis yang diuji adalah:
Ho : Variansi pada tiap kelompok sama (homogen)
H1 : Variansi pada tiap kelompok tidak sama (tidak homogen)
Dengan demikian, kehomogenan dipenuhi jika hasil uji tidak signifikan untuk suatu taraf signifikansi (α) tertentu (Biasanya α = 0,05 atau 0,01). Sebaliknya, jika hasil uji signifikan maka kenormalan tidak dipenuhi. Sama seperti untuk uji normalitas. Pada kolom Sig. terdapat bilangan yang menunjukkan taraf signifikansi yang diperoleh. Untuk menetapkan homogenitas digunakan pedoman sebagai berikut.

• Tetapkan taraf signifikansi uji, misalnya α = 0,05
• Bandingkan p dengan taraf signifikansi yang diperoleh
• Jika signifikansi yang diperoleh >α, maka variansi setiap sampel sama (homogen)
• Jika signifikansi yang diperoleh <α, maka variansi setiap sampel tidak sama (tidak homogen)

Ternyata pengujian dengan statistik Based on Mean diperoleh signifikansi 0,907, jauh lebih melebihi 0,05. dengan demikian data penelitian di atas homogen.